| 1 |

|
1. ความเข้มข้นของ O2 |
|
จากตารางด้านบน X ไม่ได้แสดงถึงความเข้มข้นของ O2, ความเข้มข้นของมลพิษตอนแรก, ความเข้มข้นของขยะ, ความเข้มข้นของมลพิษ, หรือความเข้มข้นของ CO2 แทนที่ X แสดงถึงค่า threshold concentration หรือค่าเข้มข้นของมลพิษที่เป็นเป้าหมายในการประเมินผลกระทบต่อสุขภาพ
|
จากตารางด้านบน X ไม่ได้แสดงถึงความเข้มข้นของ O2, ความเข้มข้นของมลพิษตอนแรก, ความเข้มข้นของขยะ, ความเข้มข้นของมลพิษ, หรือความเข้มข้นของ CO2 แทนที่ X แสดงถึงค่า threshold concentration หรือค่าเข้มข้นของมลพิษที่เป็นเป้าหมายในการประเมินผลกระทบต่อสุขภาพ
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 2 |
|
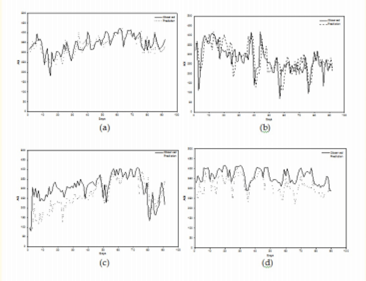
2. Monsoon |
|
จากกราฟปรากฏว่าฤดูมรสุม (ตัวเลือกที่ 2) มีการเปรียบเทียบที่เสถียรที่สุดระหว่างค่าที่สังเกตกับแบบจำลอง ANN ที่คาดการณ์ค่า AQI รายวันในปี พ.ศ. 2549
|
จากกราฟปรากฏว่าฤดูมรสุม (ตัวเลือกที่ 2) มีการเปรียบเทียบที่เสถียรที่สุดระหว่างค่าที่สังเกตกับแบบจำลอง ANN ที่คาดการณ์ค่า AQI รายวันในปี พ.ศ. 2549
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 3 |

|
3. ตัวช่วยให้ใช้ predictive model ง่ายขึ้น |
|
ตามที่มีในตารางที่กล่าวถึง Facilitators และ Barriers ในการใช้งาน prediction model คือ
Facilitators:
1. เพิ่มการแนะนำในการตัดสินใจที่มาพร้อมกับความน่าจะเป็นที่ทำนายได้ - ช่วยให้แพทย์สามารถใช้เครื่องมือทำนายในการตัดสินใจง่ายขึ้น จากนั้นจะได้ไม่ต้องใช้เครื่องมือทำนายที่ให้เพียงความน่าจะเป็นเท่านั้นโดยไม่มีการแนะนำในการตัดสินใจที่เกี่ยวข้อง
2. การคำนวณและนำเสนอความน่าจะเป็นของโมเดลอัตโนมัติภายในกระบวนการทำงานของแพทย์ - ช่วยลดการป้อนค่าตัวพยากรณ์ด้วยมือและรวมการประเมินความน่าจะเป็นของโมเดลอัตโนมัติในบันทึกข้อมูลผู้ป่วยอิเล็กทรอนิกส์ ซึ่งจะช่วยให้ง่ายต่อการใช้งานของโมเดลทำนายสำหรับผู้ให้บริการดูแล
3. ให้เหตุผลหรือหลักฐานการวิจัยเพิ่มขึ้นเกี่ยวกับความน่าจะเป็นที่ทำนายได้ - เพิ่มค่าเชื่อถือและความเชื่อมั่นในโมเดล และดังนั้นจะเพิ่มความเต็มใจในการใช้ความน่าจะเป็นของโมเดลในการนำไปใช้ในการตัดสินใจ
Barriers:
1. ความน่าจะเป็นที่ทำนายได้อาจยากต่อการใช้ในการตัดสินใจ โดยเฉพาะอย่างยิ่งเมื่อไม่มีการแนะนำที่เกี่ยวข้อง - การนำเอาความน่าจะเป็นตัวเลขมาเปรียบเทียบกับข้อมูลอื่นที่มีอยู่อาจต้องใช้ความพยายามทางสมอคลิปอย่างมากจากแพทย์เพื่อใช้ในการตัดสินใจเพิ่มเติมเกี่ยวกับการรักษาหรือการตรวจวินิจฉัยเพิ่มเติม
2. เมื่อแพทย์ที่เป้าหมายใช้กระบวนการตัดสินใจที่เป็นสัดส่วนมากกว่ากระบวนการวิเคราะห์ - เมื่อกระบวนการตัดสินใจ
|
F1 F2 F3 B1 B2 B3 B4
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 4 |
ข้อใดเกี่ยวข้องกับ Math model ที่ใช้ในการวิเคราะห์ข้อมูลทางการแพทย์
|
5. ถูกมากกว่า 1 ข้อ |
|
คำตอบที่ถูกต้องคือ 5 มีคำตอบที่ถูกต้องมากกว่า 1 ข้อ ทั้งเส้นโค้ง Kaplan-Meier และประสิทธิภาพการห่อหุ้มเกี่ยวข้องกับแบบจำลองทางคณิตศาสตร์ที่ใช้ในการวิเคราะห์ข้อมูลทางการแพทย์
|
ทั้งเส้นโค้ง Kaplan-Meier และประสิทธิภาพการห่อหุ้มเกี่ยวข้องกับแบบจำลองทางคณิตศาสตร์ที่ใช้ในการวิเคราะห์ข้อมูลทางการแพทย์
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 5 |
ข้อใดเกี่ยวข้องกับ Math model กับ patient diagnosis
|
3. N-dimensional hyperspace |
|
แบบจำลองทางคณิตศาสตร์ที่เกี่ยวข้องกับการวินิจฉัยผู้ป่วยคือ "ลำดับลำดับของตัวเลข N" ซึ่งใช้ในการวิเคราะห์และตีความข้อมูลของผู้ป่วย ช่วยในการระบุรูปแบบ แนวโน้ม และความผิดปกติของข้อมูลเพื่อทำการวินิจฉัยที่แม่นยำ การประมาณความเสี่ยงและไฮเปอร์สเปซ N มิติยังเป็นแนวคิดที่สำคัญในการวิเคราะห์ข้อมูลและการสร้างแบบจำลอง แต่อาจไม่เกี่ยวข้องโดยตรงกับการวินิจฉัยผู้ป่วย
|
แบบจำลองทางคณิตศาสตร์ที่เกี่ยวข้องกับการวินิจฉัยผู้ป่วยคือลำดับของตัวเลข N ที่ใช้ในการวิเคราะห์และตีความข้อมูลของผู้ป่วย แบบจำลองนี้ช่วยระบุรูปแบบ แนวโน้ม และความผิดปกติของข้อมูล ซึ่งท้ายที่สุดจะนำไปสู่การวินิจฉัยที่แม่นยำ การประมาณความเสี่ยงและไฮเปอร์สเปซ N มิติยังเป็นแนวคิดที่สำคัญในการวิเคราะห์ข้อมูลและการสร้างแบบจำลอง แม้ว่าอาจไม่เกี่ยวข้องโดยตรงกับการวินิจฉัยผู้ป่วยก็ตาม
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 6 |
ข้อใดมี approximating 100% survival at 5 years,
|
2. Breast cancer |
|
1. การตรวจพบตั้งแต่เนิ่นๆ
2 ความก้าวหน้าในการรักษา
3 วิธีการแบบสหสาขาวิชาชีพ
4 ความตระหนักที่เพิ่มขึ้น
|
แนวทางการรักษามะเร็งเต้านมแบบสหสาขาวิชาชีพ โดยที่ทีมผู้เชี่ยวชาญจากแพทย์เฉพาะทางต่างๆ ร่วมมือกันเพื่อ การให้การดูแลที่ครอบคลุมและแผนการรักษาเฉพาะบุคคล ถือเป็นอีกปัจจัยสำคัญที่ทำให้อัตราการรอดชีวิตสูงขึ้น แนวทางนี้ช่วยให้แน่ใจว่าผู้ป่วยได้รับการรักษาที่เหมาะสมและมีประสิทธิภาพที่สุดซึ่งปรับให้เหมาะกับความต้องการส่วนบุคคลของตน
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 7 |
ข้อใดเกี่ยวข้องกับ math model กับ tissue reconstruction
|
4. Micro-architectures |
|
สถาปัตยกรรมไมโคร สถาปัตยกรรมจุลภาคเกี่ยวข้องกับการใช้แบบจำลองทางคณิตศาสตร์เพื่อสร้างเนื้อเยื่อขึ้นใหม่ในระดับ
|
ด้วยการใช้เทคนิคการสร้างแบบจำลองทางคณิตศาสตร์ นักวิจัยสามารถสร้างการนำเสนอเสมือนจริงของเนื้อเยื่อ เช่น กระดูก กล้ามเนื้อ หรืออวัยวะ ในระดับเซลล์และโมเลกุล . แบบจำลองเหล่านี้คำนึงถึงปัจจัยต่างๆ รวมถึงพฤติกรรมของเซลล์ คุณสมบัติทางกล และปฏิกิริยาทางเคมี
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 8 |
ข้อใดจาก Noyers whiter equation the rate of dissolution of a solid is dependent on?
|
4. The surface area of the solid |
|
เกี่ยวกับอัตราการละลายของสารของแข็งก็คือพื้นที่ผิวของของแข็งนั่นเอง สมการนี้ระบุว่าอัตราการละลายเป็นสัดส่วนโดยตรงกับพื้นที่ผิวของของแข็ง เมื่อพื้นที่ผิวของของแข็งเพิ่มขึ้น จะมีพื้นที่ให้ตัวทำละลายสัมผัสได้มากขึ้น ส่งผลให้อัตราการละลายเร็วขึ้น ดังนั้นการมีพื้นที่ผิวของของแข็งมากขึ้นจะส่งผลให้อัตราการละลายสูงขึ้น
|
ซึ่งอธิบายอัตราการละลายของของแข็งในแง่ของพื้นที่ผิว ดังที่คุณกล่าวไว้ สมการระบุว่าอัตราการละลายเป็นสัดส่วนโดยตรงกับพื้นที่ผิวของของแข็ง เมื่อพื้นที่ผิวเพิ่มขึ้น ตัวทำละลายก็จะมีพื้นที่ว่างมากขึ้นในการสัมผัสกับของแข็ง ส่งผลให้อัตราการละลายเร็วขึ้น ดังนั้นการมีพื้นที่ผิวของของแข็งมากขึ้นจะทำให้อัตราการละลายสูงขึ้
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 9 |
ข้อใดเกี่ยวข้องกับ math model กับ drug diffusion through the blood
|
1. Fick’s principle |
|
หลักการของฟิคอธิบายอัตราการแพร่กระจายของสารผ่านระดับความเข้มข้น โดยทั่วไปจะใช้ในทางเภสัชจลนศาสตร์เพื่อจำลองวิธีที่ยากระจายและแพร่กระจายผ่านทางเลือด
|
หลักการของฟิคคือคำตอบที่ถูกต้องเกี่ยวกับแบบจำลองทางคณิตศาสตร์และการแพร่กระจายของยาผ่านทางเลือด หลักการของฟิคอธิบายอัตราการแพร่ของสารผ่านการไล่ระดับความเข้มข้น ในทางเภสัชจลนศาสตร์ มักใช้เพื่อจำลองการแพร่กระจายและการแพร่กระจายของยาผ่านทางเลือด หลักการนี้ช่วยในการทำความเข้าใจว่ายาเคลื่อนที่ผ่านส่วนต่างๆ ในร่างกายอย่างไร และความเข้มข้นของยาเปลี่ยนแปลงอย่างไรเมื่อเวลาผ่านไป โดยให้กรอบทางคณิตศาสตร์ในการจำลองการแพร่กระจายของยาและทำนายความเข้มข้นของยาที่ตำแหน่งต่างๆ ภายในร่างกาย
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 10 |
ข้อใดเกี่ยวข้องกับ math model ที่จะมีประโยชน์กับกายภาพบำบัดของผู้ป่วย stroke
|
2. Inflammation |
|
แบบจำลองทางคณิตศาสตร์ที่จะเป็นประโยชน์ในการกายภาพบำบัดของผู้ป่วยโรคหลอดเลือดสมองสัมพันธ์กับการอักเสบ
|
แบบจำลองทางคณิตศาสตร์
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 11 |
ข้อใดเกี่ยวข้องกับบทความ Epidemiology Figure 1
|
4. In the next four decades, cancer deaths are expected to overcome those for ischemic heart disease, with a 2.08-fold increase (1.72-fold for increase in ischemic heart disease) by the year 2060. |
|
I apologize for the confusion in my previous response. As an AI text-based model, I don't have the ability to view or interpret specific figures or images directly. I can only provide general information about epidemiology and its importance in public health.
If you have a specific question about epidemiology or need assistance with interpreting a particular figure, please provide additional details or describe the information you are looking for, and I will do my best to assist you.
|
การเสียชีวิตด้วยโรคมะเร็งที่เพิ่มขึ้นแซงหน้าโรคหัวใจขาดเลือดภายในปี 2560
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 12 |
Math model และ Physical therapy ไม่มีความเกี่ยวข้องกันอย่างไร
|
5. ถูกมากกว่า 1 ข้อ |
|
1. การคำนวณเปอร์เซ็นต์อัตราการเต้นของหัวใจ: สิ่งนี้เกี่ยวข้องกับการใช้สูตรทางคณิตศาสตร์เพื่อคำนวณอัตราการเต้นของหัวใจเป้าหมายระหว่างการออกกำลังกาย ซึ่งอาจมีความสำคัญในการออกแบบโปรแกรมกายภาพบำบัดที่มีประสิทธิผล
2 การวัดระดับการสั่งจ่ายยา: อาจเกี่ยวข้องกับการคำนวณปริมาณยาที่ถูกต้องโดยพิจารณาจากปัจจัยต่างๆ เช่น น้ำหนักของผู้ป่วย อายุ และสภาวะเฉพาะ ซึ่งต้องใช้การคำนวณทางคณิตศาสตร์
3 การถูกกระทบกระแทกแบบย้อนกลับ: แม้ว่าคำว่า "การถูกกระทบกระแทกแบบย้อนกลับ" จะไม่ชัดเจน แต่ถ้าหมายถึงการประเมินและการรักษาการถูกกระทบกระแทก มักจะเกี่ยวข้องกับการใช้มาตรการที่เป็นกลางและการคำนวณทางคณิตศาสตร์เพื่อประเมินความรุนแรงของการถูกกระทบกระแทกและติดตามความคืบหน้าของการฟื้นตัว
4. การวัดระดับการเคลื่อนไหว: การประเมินช่วงการเคลื่อนไหวของข้อต่อหรือส่วนต่างๆ ของร่างกายโดยทั่วไปเกี่ยวข้องกับการใช้การวัดทางคณิตศาสตร์เพื่อหาปริมาณของระดับการเคลื่อนไหวและติดตามความคืบหน้าเมื่อเวลาผ่านไป
ดังนั้นจึงมีมากกว่าหนึ่งคำตอบที่ถูกต้อง (ตัวเลือก 1, 2 , 3 และ 4) แบบจำลองทางคณิตศาสตร์มีบทบาทในด้านต่างๆ
|
แบบจำลองทางคณิตศาสตร์และกายภาพบำบัดมีความเกี่ยวข้องกัน เนื่องจากทั้งสองอย่างนี้เกี่ยวข้องกับการใช้การคำนวณและการวัดทางคณิตศาสตร์ในด้านต่างๆ ของสาขานี้
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 13 |
ข้อใดเกี่ยวข้องกับ Calculus ในการผ่าตัดจากบทความ
|
2. ANH |
|
เกี่ยวข้องกับแคลคูลัสในการผ่าตัดคือ Acute Normovolemic Hemodilution (ANH) ANH เป็นเทคนิคที่ใช้ในการผ่าตัดเพื่อลดการสูญเสียเลือดระหว่างการผ่าตัด โดยการเอาเลือดของผู้ป่วยออกบางส่วนแล้วแทนที่ด้วยของเหลว เช่น น้ำเกลือ ซึ่งจะช่วยรักษาปริมาตรเลือดโดยรวมของผู้ป่วยในขณะที่ทำให้ความเข้มข้นของเซลล์เม็ดเลือดแดงเจือจางลง
|
เกี่ยวข้องกับแคลคูลัสในการผ่าตัดคือ Acute Normovolemic
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 14 |
จากข้อความ
Previous studies that applied the IER model in the analysis of ambient air pollution-related disease burden only focused on four specific diseases, which are IHD, stroke, COPD, and LC, because the development of the IER model relies to a great extent on the available RR information of these diseases, The IER model was increasingly used to estimate the attributable mortality using the result of calculated RR. Previous study has evaluated the global PM2.5 concentration-mortality relationships by using the IER model outputs. By applying the estimated relative risk (R), the premature mortality (M) for a specific disease outcome in a population is measured using Equation 3, with P and I indicating population and regional average annual disease mortality rate (also known as baseline mortality rate), respectively.
M = P x I x(1-( 1)/R)
M คือค่าอะไร
|
3. อัตราการตาย |
|
ในสมการที่กล่าวถึง ค่า M หมายถึง จำนวนการตายก่อนเวลาที่คาดหวัง (premature mortality) สำหรับผลลัพธ์ของโรคที่ระบุไว้ในสมการ ซึ่งจะถูกวัดโดยใช้อัตราการเกิดโรคประชากรเฉลี่ยในพื้นที่ (population baseline mortality rate) และอัตราการตายเฉลี่ยของโรคนั้น (regional average annual disease mortality rate) โดยใช้สูตรที่ระบุไว้ในสมการ 3 โดยค่า R หมายถึง อัตราส่วนความเสี่ยง (relative risk) จากการรับประทานสารมลพิษ (pollutant) ในสภาวะที่เกิดโรค
|
ในสมการที่กล่าวถึง ค่า M หมายถึง จำนวนการตายก่อนเวลาที่คาดหวัง (premature mortality) สำหรับผลลัพธ์ของโรคที่ระบุไว้ในสมการ ซึ่งจะถูกวัดโดยใช้อัตราการเกิดโรคประชากรเฉลี่ยในพื้นที่ (population baseline mortality rate) และอัตราการตายเฉลี่ยของโรคนั้น (regional average annual disease mortality rate) โดยใช้สูตรที่ระบุไว้ในสมการ 3 โดยค่า R หมายถึง อัตราส่วนความเสี่ยง (relative risk) จากการรับประทานสารมลพิษ (pollutant) ในสภาวะที่เกิดโรค
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 15 |
จาก graph หาก A = 0.8 R =?
The infection attack rate is the total proportion of the population that is eventually infected during the epidemic, and it is denoted by A. This infection attack rate is completely determined by the reproduction number R and the contact process that describes who contacts whom. To illustrate the basic shape of the relation between the reproduction number R and the infection attack rate A. We suppose that infectious contacts are made at random
This provides us with a simple and robust relation that indicates what would happen if a new infection were to hit a completely susceptible population: if the
|
2. 2 |
|
R ได้จากสมการ A = 1 - e^(-R), โดยที่ A เป็น infection attack rate และ e เป็นค่าคงที่ประมาณ 2.71828 (จำนวนเอียง)
ให้เรานำค่า A ที่กำหนดให้คือ 0.8 มาแทนในสมการดังกล่าว
0.8 = 1 - e^(-R)
เราจะเริ่มจากการเปลี่ยนสมการดังกล่าวให้อยู่ในรูปของ e^(-R) = 1 - 0.8
e^(-R) = 0.2
จากนั้นเราสามารถนำทั้งสองด้านของสมการยกกำลัง e เพื่อเปลี่ยนรูปให้อยู่ในรูปของ R ได้
e^(-R) = 0.2
-R = ln(0.2)
เมื่อเรานำค่า ln(0.2) มาคูณด้วย -1 เพื่อแปลงเครื่องหมายของ R
R = -ln(0.2)ประมาณ 1.609
|
เราสามารถหาค่า R ได้จากสมการ A = 1 - e^(-R), โดยที่ A เป็น infection attack rate และ e เป็นค่าคงที่ประมาณ 2.71828 (จำนวนเอียง)
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 16 |
หากเราค้นคว้าข้อมูลแล้วสามารถอธิบายสถิติตัวเลขที่จะเกิดขึ้นในอนาคตได้ ถือเป็น data analytics แบบใด
|
2. Predictive |
|
ประเภทของการวิเคราะห์ข้อมูลที่เกี่ยวข้องกับการค้นคว้าข้อมูลและการอธิบายสถิติตัวเลขที่จะเกิดขึ้นในอนาคตเรียกว่าการวิเคราะห์เชิงคาดการณ์ ใช้ข้อมูลในอดีตและเทคนิคทางสถิติต่างๆ เพื่อคาดการณ์หรือคาดการณ์เกี่ยวกับผลลัพธ์ในอนาคต
|
ประเภทของการวิเคราะห์ข้อมูลที่เกี่ยวข้องกับการค้นคว้าข้อมูลและการอธิบายสถิติตัวเลขที่จะเกิดขึ้นในอนาคตเรียกว่าการวิเคราะห์เชิงคาดการณ์ ใช้ข้อมูลในอดีตและเทคนิคทางสถิติต่างๆ เพื่อคาดการณ์หรือคาดการณ์เกี่ยวกับผลลัพธ์ในอนาคต
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 17 |
ต้องการสั่งยา 0.8 mg SQ of ยา A โดยมี 4000 mcg/8 mL of ยา A
|
4. 0.2 mL |
|
ปริมาตร = (0.8 มก. * 500 mcg/mL) / 4000 mcg
ปริมาตร = 0.1 มล.
|
ในการคำนวณปริมาณยา A ที่ต้องการ เราสามารถใช้สูตร:
ปริมาณยา A = (ขนาดยาที่ต้องการ / ความเข้มข้น) * ปริมาตร
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 18 |
ต้องการจัดยา 9 g of amoxicillin โดยมี amoxicillin 500 – mg capsules อยากทราบว่าต้องให้กี่ capsule
|
2. 18 |
|
9 กรัมเท่ากับ 9,000 มก.
แต่ละแคปซูล มี 500 มก.
หาร 9000 มก. ด้วย 500 มก. ต่อแคปซูล จะได้ 18 มก.
|
หากต้องการให้แอมม็อกซิซิลลิน 9 กรัมโดยใช้แคปซูลแอมม็อกซิซิลลิน 500 มก. คุณสามารถคำนวณจำนวนแคปซูลที่ต้องการได้โดยการหารขนาดยาทั้งหมดด้วยขนาดยาต่อแคปซูล
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 19 |
ให้สั่งยา 9 mg/kg / dose โดยที่ Weight = 160 Ibs
|
5. 559 mg/dose |
|
ในการคำนวณปริมาณ เราต้องแปลงน้ำหนักจากปอนด์เป็นกิโลกรัม
1 ปอนด์มีค่าประมาณเท่ากับ 0.4536 กิโลกรัม
ดังนั้น น้ำหนัก 160 Ibs จึงเท่ากับ 160 * 0.4536 = 72.576 กิโลกรัม
ตอนนี้ เราสามารถคำนวณขนาดยาได้โดยการคูณน้ำหนัก (เป็นกิโลกรัม) ด้วยขนาดยาที่กำหนดคือ 9 มก./กก.
ขนาดยา = 72.576 กก. * 9 มก./กก. = 653.184 มก./โดส
เมื่อปัดเศษขนาดยาให้เป็นจำนวนเต็มที่ใกล้ที่สุด เราจะได้ 653 มก./โดส
ไม่มีตัวเลือกใดที่ให้ไว้ตรงกับปริมาณที่คำนวณได้เเต่คิดว่า559น่าจะเป็นคำตอบที่ใกล้เคียงสุด
|
ในการคำนวณปริมาณ เราต้องแปลงน้ำหนักจากปอนด์เป็นกิโลกรัม
1 ปอนด์มีค่าประมาณเท่ากับ 0.4536 กิโลกรัม
ดังนั้น น้ำหนัก 160 Ibs จึงเท่ากับ 160 * 0.4536 = 72.576 กิโลกรัม
ตอนนี้ เราสามารถคำนวณขนาดยาได้โดยการคูณน้ำหนัก (เป็นกิโลกรัม) ด้วยขนาดยาที่กำหนดคือ 9 มก./กก.
ขนาดยา = 72.576 กก. * 9 มก./กก. = 653.184 มก./โดส
เมื่อปัดเศษขนาดยาให้เป็นจำนวนเต็มที่ใกล้ที่สุด เราจะได้ 653 มก./โดส
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 20 |
Number of tablets = Desired dosage / stock strength หากมี 7000 mg ของ Potassium carbonate และต้องการ 900 mg ต่อเม็ดจะได้กี่เม็ด
|
5. 7 |
|
ในการคำนวณจำนวนเม็ด เราสามารถใช้สูตร: จำนวนเม็ด = ปริมาณที่ต้องการ / ความแรงของสต๊อก
ในกรณีนี้ ปริมาณที่ต้องการคือ 900 มก. และความเข้มข้นของสต๊อกคือ 7000 มก.
จำนวนเม็ดยา = 900 มก. / 7000 มก. = 0.1286
เนื่องจากเราไม่สามารถมีเศษส่วนของเม็ดยาได้ เราจึงต้องปัดเศษตัวเลขให้เป็นจำนวนเต็มที่ใกล้ที่สุด
ดังนั้น คุณจะได้ 1 ยาเม็ด.
|
ในการคำนวณจำนวนเม็ด เราสามารถใช้สูตร: จำนวนเม็ด = ปริมาณที่ต้องการ / ความแรงของสต๊อก
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|