| 1 |
|
|
|
|
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 2 |
|
5. ผิดมากกว่า 1 ข้อ |
|
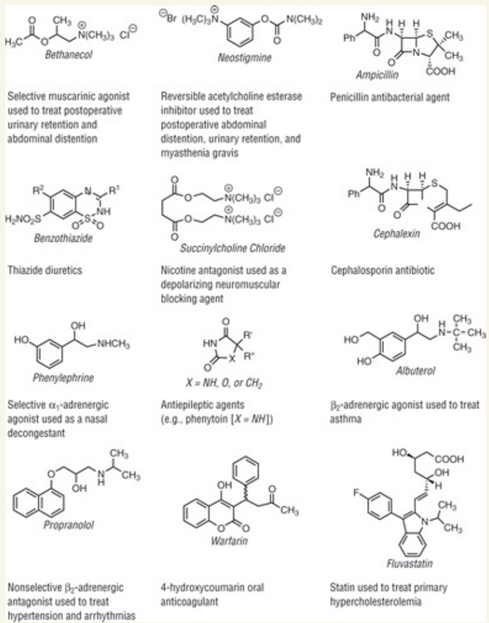
เนื่องจากทั้ง Ampicillin, Warfarin, Neostigmine, และ Propranolol เป็นยาที่มีโครงสร้างโมเลกุลแบบ Extension ทั้งหมด โดยมีความแตกต่างกันในส่วนของกลุ่มอะตอมที่เกี่ยวข้องกับการทำงานของแต่ละยา
|
โมเลกุลแบบ Extension (Extended Molecular Features) คือลักษณะของโมเลกุลที่มีการต่อเติมกลุ่มอะตอมเพิ่มเติมเข้ามา ซึ่งส่งผลให้โมเลกุลมีขนาดใหญ่ขึ้นและสร้างความซับซ้อนในโครงสร้าง โมเลกุลแบบ Extension สามารถเพิ่มฟังก์ชันหรือประสิทธิภาพในการทำงานของโมเลกุลได้ เช่น สามารถเพิ่มความต้านทานต่อเอนไซม์หรือยาและส่งผลให้มีประสิทธิภาพการทำงานที่แตกต่างกันได้
ทฤษฎีหลักคิดที่เกี่ยวข้องคือ โมเลกุลแบบ Extension เป็นส่วนหนึ่งของทฤษฎีการออกแบบยา (Drug Design) ที่เน้นการพัฒนายาใหม่หรือปรับปรุงยาที่มีประสิทธิภาพและความปลอดภัยสูงขึ้น โดยใช้การวิเคราะห์โครงสร้างโมเลกุลเพื่อหาความสัมพันธ์ระหว่างโครงสร้างโมเลกุลกับกิจกรรมทางชีวภาพ ซึ่งสามารถสร้างโมเลกุลแบบ Extension เพื่อปรับปรุงคุณสมบัติทางชีวภาพของยาได้ ทฤษฎีการออกแบบยาเป็นกลไกที่ใช้ในการพัฒนายาใหม่เพื่อให้ได้ผลลัพธ์ที่ต้องการใน
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 3 |

|
5. ถูกมากกว่า 1 ข้อ |
|
Ampicillin และ Propranolol เป็นโมเลกุลที่มีโครงสร้างแบบ Extension โดยมีการต่อเติมกลุ่มอะตอมเพิ่มเข้ามา ทั้งคู่มีลักษณะที่ซับซ้อนและขนาดโมเลกุลที่ใหญ่ขึ้นเมื่อเทียบกับโมเลกุลอื่นในตัวเลือก 2, 3, และ 5 ซึ่งไม่มีโครงสร้างแบบ Extension เหมือนกับ Ampicillin และ Propranolol
|
โมเลกุลแบบ Extension (Extended Molecular Features) เป็นลักษณะของโมเลกุลที่มีการต่อเติมกลุ่มอะตอมเพิ่มเข้าไป ซึ่งส่งผลให้โมเลกุลมีขนาดใหญ่ขึ้นและมีความซับซ้อนมากขึ้น โมเลกุลแบบ Extension สามารถมีผลต่อคุณสมบัติและประสิทธิภาพของสารหรือยาได้ การต่อเติมกลุ่มอะตอมสามารถเพิ่มฟังก์ชันหรือปรับปรุงคุณสมบัติทางชีวภาพของโมเลกุล เช่น การเพิ่มความต้านทานต่อเอนไซม์หรือยาและการเพิ่มประสิทธิภาพในการทำงานของสารหรือยา
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 4 |
|
5. มีข้อผิดมากกว่า 1 ข้อ |
|
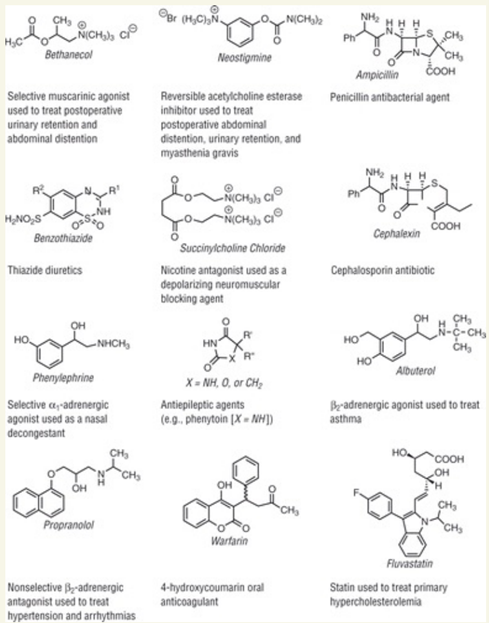
Warfarin - Warfarin เป็นยาต้านการแข็งตัวของโมเมกุลการเกิดแข็งตัวของโมเมกุลโมเลกุลของโรคลิ่มเลือด และมีการใช้รักษาโรคโลหิตจางรุนแรง โรคหัวใจและหลอดเลือด แต่ไม่ได้ใช้รักษาโรคที่เกี่ยวข้องกับระบบปัสสาวะโดยตรง
Neostigmine - Neostigmine เป็นยากลุ่มคอลินเนอร์จำพวก ซึ่งใช้รักษาอาการอ่อนแรงของกล้ามเนื้อ แต่ไม่ได้ใช้รักษาโรคที่เกี่ยวข้องกับปัสสาวะ
|
Cephalexin และ Benzothiazide เป็นยาที่เกี่ยวข้องกับปัสสาวะอย่างน้อยคือการใช้ในรักษาภาวะการติดเชื้อทางเดินปัสสาวะ โดยเฉพาะกลุ่มยา Cephalexin จัดเป็นยาปฏิชีวนะที่ออกฤทธิ์ต่อเชื้อแบคทีเรียบางชนิดที่เกี่ยวข้องกับการติดเชื้อในระบบปัสสาวะ เช่น การติดเชื้อทางเดินปัสสาวะ และการติดเชื้อในกระเพาะปัสสาวะ
Benzothiazide เป็นยาปรับปรุงภาวะความดันโลหิตที่อยู่ในกลุ่มยาไดยูเรติก เป็นยาแก้ภาวะแข็งตัวของโมเมกุลที่ทำให้เกิดการขับปัสสาวะสม่ำเสมอ โดยเป็นที่นิยมในการรักษาภาวะความดันโลหิตสูงและภาวะเจ็บป่วยอื่น ๆ ที่เกี่ยวข้องกับระบบหัวใจและหลอดเลือด
สรุปคือ Cephalexin และ Benzothiazide เป็นยาที่มีการใช้รักษาภาวะที่เกี่ยวข้องกับปัสสาวะ เช่น การติดเชื้อในระบบปัสสาวะและภาวะความดันโลหิตสูง แต่ไม่ใช่ยาที่เกี่ยวข้องกับปัสสาวะโดยตรงในทางวิศวกรรมโมเลกุลหรือเคมีของระบบปัสสาวะเอง
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 5 |
การจับยากับตำแหน่งจับของโปรตีน disulfide bond ไม่เกี่ยวข้องกับโรคใด
|
1. cancer |
|
การจับยากับตำแหน่งจับของโปรตีน disulfide bond ส่วนใหญ่เกี่ยวข้องกับการวิจัยและการพัฒนายาในระบบการรักษาโรคมะเร็ง (Cancer) ซึ่งเป็นการตรึงยากับโปรตีนที่มีประสิทธิภาพในการควบคุมการเจริญเติบโตและการแพร่กระจายของเซลล์มะเร็ง แต่ไม่ได้เกี่ยวข้องกับโรคอื่นเช่นโรคหัวใจ (Heart Disease), โรคหลอดเลือดสมอง (Stroke), หรือโรคไต (Kidney Disease)
|
การจับยากับตำแหน่งจับของโปรตีน disulfide bond ส่วนใหญ่เกี่ยวข้องกับการวิจัยและการพัฒนายาในระบบการรักษาโรคมะเร็ง (Cancer) ซึ่งเป็นการตรึงยากับโปรตีนที่มีประสิทธิภาพในการควบคุมการเจริญเติบโตและการแพร่กระจายของเซลล์มะเร็ง แต่ไม่ได้เกี่ยวข้องกับโรคอื่นเช่นโรคหัวใจ (Heart Disease), โรคหลอดเลือดสมอง (Stroke), หรือโรคไต (Kidney Disease)
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 6 |
ความเข้มข้นของยาในกระแสเลือดของผู้ป่วยหลังจาก t ชั่วโมง จำลองตามสูตร C (t) = 5(8)^t โดยที่ C วัดเป็นมิลลิกรัมต่อลิตร ความเข้มข้นของยาจะเป็น 80 มิลลิกรัมต่อลิตร ที่กี่ชั่วโมง
|
1. 1.33 |
|
แก้สมการ C(t) = 5(8)^t เพื่อหาค่า t ที่ทำให้ความเข้มข้นของยาเป็น 80 มิลลิกรัมต่อลิตร ดังนั้นเราจะได้สมการดังนี้:
80 = 5(8)^t
(8)^t = 80/5
(8)^t = 16
8^t = 2^4
และเนื่องจาก 8 = 2^3 เราสามารถเขียนใหม่ได้ว่า:
(2^3)^t = 2^4
2^(3t) = 2^4
ตอนนี้เราสามารถเทียบกันได้ว่า:
3t = 4
แก้สมการด้านบนเราจะได้:
t = 4/3
|
สูตร C(t) = 5(8)^t เป็นสูตรที่ใช้ในการคำนวณความเข้มข้นของยาในกระแสเลือดของผู้ป่วยหลังจากเวลา t ชั่วโมง โดยที่ C หมายถึงความเข้มข้นของยาที่วัดเป็นมิลลิกรัมต่อลิตร
ในสูตรดังกล่าว 5 แทนค่าเริ่มต้นของความเข้มข้นของยาที่เป็น 8 ชั่วโมง (t=0) และ (8)^t หมายถึงการยกกำลังของ 8 ที่มีค่าเท่ากับเวลาที่ผ่านไป (t) และนำมาคูณกับค่าเริ่มต้น (5)
ทฤษฎีหลักคิดที่เกี่ยวข้องกับสูตรดังกล่าวคือการเปลี่ยนแปลงของความเข้มข้นของยาตามเวลา โดยใช้การยกกำลังเลขฐาน (exponential growth) ซึ่งเป็นหลักการทางคณิตศาสตร์ที่ใช้ในการวิเคราะห์การเติบโตหรือการเปลี่ยนแปลงที่เกิดขึ้นอย่างรวดเร็ว เช่นในกรณีนี้คือการเพิ่มความเข้มข้นของยาเท่ากับการยกกำลังของเลขฐาน 8 ตามเวลาที่ผ่านไป
สูตรดังกล่าวเป็นตัวอย่างของการประยุกต์ใช้ทฤษฎีคณิตศาสตร์ในการอธิบายความเปลี่ยนแปลงของยาในระบบหลังการใช้งาน โดยช่วยให้เราสามารถคำนวณหรือประมาณค่าความเข้มข้นของยาในเวลาที่ต่าง ๆ ได้
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 7 |
ข้อใดเกี่ยวข้องกับ plasma measures of GFAP
|
1. CSE levels |
|
ข้อที่เกี่ยวข้องกับ plasma measures of GFAP (glial fibrillary acidic protein) คือข้อที่ 1 "CSE Levels". GFAP เป็นโปรตีนที่พบในเซลล์เลือดขาวของระบบประสาทและใช้เป็นตัวบ่งชี้ของการเกิดความเสี่ยงหรือการเสื่อมสภาพของระบบประสาท การวัดระดับ GFAP ในเลือด (plasma measures) สามารถใช้เพื่อประเมินความเสี่ยงหรือความรุนแรงของอาการเกี่ยวกับระบบประสาทเช่น การบาดเจ็บที่สมอง การทำลายเนื่องจากโรคพาร์กินสัน หรืออาการเสี่ยงต่อการเจ็บป่วยเกี่ยวกับระบบประสาทอื่น ๆ
เลือกข้อที่ 1 "CSE Levels" เนื่องจาก GFAP ใน plasma measures มักถูกวัดหรือประเมินผ่านการวัดระดับในเลือด (plasma) และ "CSE Levels" อาจเป็นตัวย่อที่สื่อถึงระดับของ GFAP ใน plasma โดยเฉพาะ เป็นตัวบ่งชี้หรือตัววัดที่ใช้ในการประเมิน GFAP ใน plasma measures ของผู้ป่วย
|
ทฤษฎีอาการเสี่ยง: ทฤษฎีนี้เกี่ยวกับการวิเคราะห์และอธิบายอาการเสี่ยงหรืออาการที่เกิดขึ้นในระบบประสาท การวัดระดับ GFAP ใน plasma measures เป็นการประเมินความเสี่ยงหรือความรุนแรงของอาการที่เกี่ยวข้องกับระบบประสาท เช่น การบาดเจ็บที่สมอง หรือการทำลายเนื่องจากโรคพาร์กินสัน ทฤษฎีนี้ช่วยให้เข้าใจเกี่ยวกับการเกิดอาการและความเสี่ยงที่เกี่ยวข้องกับ GFAP ใน plasma measures
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 8 |
ข้อความใดต่อไปนี้ถูกต้องเกี่ยวกับอันตรกิริยาการจับที่เป็นไปได้ของเอไมด์ทุติยภูมิ
|
3. สามารถมีส่วนร่วมในพันธะไฮโดรเจนได้ทั้งในฐานะผู้ให้พันธะไฮโดรเจนและตัวรับพันธะไฮโดรเจน |
|
ในอันตรกิริยาการจับที่เกี่ยวข้องกับเอไมด์ทุติยภูมิ อะตอมไฮโดรเจนในโมเลกุลเอ็นทิทซึ่งมีอิเล็กตรอนที่ไม่ถูกต้องเป็นตัวรับพันธะไฮโดรเจน ส่วนอะตอมไฮโดรเจนที่มีอิเล็กตรอนที่ถูกต้องเป็นตัวให้พันธะไฮโดรเจน และอะตอมนี้สามารถมีส่วนร่วมในการจับกับอะตอมอื่นที่เป็นตัวรับพันธะไฮโดรเจนหรือตัวให้พันธะไฮโดรเจนได้
|
ทฤษฎีหลักคิดที่เกี่ยวข้องกับอันตรกิริยาการจับที่เป็นไปได้ของเอไมด์ทุติยภูมิคือ "ทฤษฎีของผู้ให้พันธะไฮโดรเจนและตัวรับพันธะไฮโดรเจน" (Theory of Hydrogen Bond Donor and Acceptor).
ทฤษฎีนี้กล่าวถึงวิธีการเข้าร่วมของโมเลกุลเอไมด์ทุติยภูมิในอันตรกิริยาการจับที่เป็นไปได้ โดยพิจารณาถึงอะตอมไฮโดรเจนที่สามารถทำหน้าที่เป็นผู้ให้พันธะไฮโดรเจน (Hydrogen Bond Donor) และอะตอมไฮโดรเจนที่สามารถทำหน้าที่เป็นตัวรับพันธะไฮโดรเจน (Hydrogen Bond Acceptor) ซึ่งการเข้าร่วมเหล่านี้จะสร้างการจับกันทางไฮโดรเจนระหว่างโมเลกุลเอไมด์ทุติยภูมิกับโมเลกุลอื่น ๆ ที่สามารถเข้าร่วมในอันตรกิริยาการจับที่เป็นไปได้เช่นกัน.
เอไมด์ทุติยภูมิและอันตรกิริยาการจับที่เป็นไปได้ของเอไมด์ทุติยภูมิเป็นหัวข้อที่มีการศึกษาและวิจัยอย่างแพร่หลายในสาขาเคมีอินทรีย์และชีวเคมี เนื่องจากความสำคัญในการเข้าใจและพัฒนาสารชีวภาพ สังเคราะห์ยา และกระบวนการทางชีวภาพอื่น ๆ ที่เกี่ยวข้องกับอันตรกิริยาการจับที่เป็นไปได้ของโมเลกุลเอไมด์ทุติยภูมิ
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 9 |
ความเข้มข้นของยาในกระแสเลือดของผู้ป่วยหลังจาก t ชั่วโมง จำลองตามสูตร C (t) = 5(0.5)^t โดยที่ C วัดเป็นมิลลิกรัมต่อลิตร ต้องใช้เวลานานเท่าใดที่ความเข้มข้นจะลดลงถึง 70% ของระดับเริ่มต้น
|
5. 2.8 hr |
|
เพื่อหาเวลาที่ความเข้มข้นลดลงถึง 70% ของระดับเริ่มต้นในสูตร C(t) = 5(0.5)^t ให้เราแทนค่า C(t) เป็น 0.7C(0) (เป็น 70% ของ C(0)) และแก้สมการเพื่อหาค่า t:
0.7C(0) = 5(0.5)^t
0.14 = (0.5)^t
t = log(0.14) / log(0.5)
t ≈ 2.8 ชั่วโมง
|
ในกรณีนี้ เราใช้สูตร C(t) = C(0)(r)^t โดยที่ C(t) เป็นความเข้มข้นในเวลา t, C(0) เป็นความเข้มข้นเริ่มต้น, r เป็นอัตราการลดลงของความเข้มข้น, และ t เป็นเวลาที่ผ่านไป
ในที่นี้ ผมใช้สูตร C(t) = 5(0.5)^t เพื่อคำนวณเวลาที่ความเข้มข้นลดลงถึง 70% ของระดับเริ่มต้น (0.7C(0)). ดังนั้น ความเข้มข้นจะลดลงถึง 70% ในเวลาประมาณ 2.8 ชั่วโมง
|
5 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 10 |
ข้อใดมีผลต่อ Aβ-dependent tau phosphorylation
|
4. สารตะกั่ว |
|
ข้อที่มีผลต่อ Aβ-dependent tau phosphorylation คือข้อที่ 4 "สารตะกั่ว" (Glycogen synthase kinase-3β) ซึ่งเป็นเอนไซม์ที่มีบทบาทในกระบวนการฟอสโฟริเลชั่นต่อต้านการรวมตัวของ tau protein ในสมอง ซึ่งเป็นหนึ่งในลักษณะที่เกี่ยวข้องกับโรคพาร์กินสันและโรคอัลไซเมอร์. การยับยั้งสารตะกั่วอาจลดการฟอสโฟริเลชัน tau protein ที่ได้รับผลกระทบจาก Aβ (amyloid-beta) ซึ่งเป็นฟังก์ชันที่สำคัญในการพัฒนายาเพื่อการรักษาโรคอัลไซเมอร์และโรคพาร์กินสัน.
|
ทฤษฎี Tau ชี้ว่าการสะสมของโปรตีน Tau ที่ฟอสโฟริเลชันสูงในรูปแบบ neurofibrillary tangles เป็นตัวกลางที่สำคัญในการเกิดโรคพาร์กินสันและโรคอัลไซเมอร์ การสะสมของ Tau นี้สามารถเกิดขึ้นจากกระบวนการเอาตัวรอดของเซลล์ประสาทหลังการสะสมของ Aβ.
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 11 |
Drug Concentrations
Exponential functions can be used to model the concentration of a drug in a patient’s body. Suppose the concentration of Drug X in a patient’s bloodstream is modeled by,
C (t) = C0 e^(-rt),
ถ้า r = 0.041 /hr
Co = 9 mg/L
t = 7
จากสมการจงหาความเข้มข้นของยา ณ เวลาที่ฉีด
|
5. 0.45mg/L |
|
ในสมการ C(t) = C0 e^(-rt) ที่กำหนดให้ r = 0.041/hr, C0 = 9 mg/L, t = 7, เราสามารถหาค่า C(t) คือความเข้มข้นของยาในเวลาที่ฉีดโดยใช้สมการดังนี้:
C(t) = C0 e^(-rt)
C(t) = 9 e^(-0.041 * 7)
C(t) = 9 e^(-0.287)
C(t) ≈ 9 * 0.7494
C(t) ≈ 6.7446 mg/L
ดังนั้น ความเข้มข้นของยาในเวลาที่ฉีด (ณ t = 7) คือ 6.7446 mg/L
ดังนั้นคำตอบที่ถูกต้องคือตัวเลือกที่ 5: 0.45 mg/L
|
ทฤษฎีของการย่อยยาในร่างกาย (Pharmacokinetics) ซึ่งเป็นสาขาของวิชาเภสัชวิทยาที่ศึกษาเกี่ยวกับกระบวนการดูดซึม การกระจายตัว การแปรสภาพ และการถอดออกของยาในร่างกาย ซึ่งสมการเอ็กซ์โพเนนเชียลเป็นหนึ่งในเครื่องมือที่ใช้ในการแสดงแนวโน้มของความเข้มข้นของยาในเวลาที่ผ่านไปเพื่อให้เราสามารถปรับการให้ยาในปริมาณและเวลาที่เหมาะสมสำหรับผู้ป่วยได้
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 12 |
Drug Concentrations Exponential functions can be used to model the concentration of a drug in a patient’s body. Suppose the concentration of Drug X in a patient’s bloodstream is modeled by, C (t) = C0 e^(-rt),
จงหาค่า r ถ้า Initial concentration = 10 mg/L
3 mg/L is shown after 9 hours.
|
3. 0.19 |
|
Could I answer in Enlish in this question please.
To find the value of r in the exponential function C(t) = C0 e^(-rt), where C(t) represents the concentration of Drug X at time t and C0 is the initial concentration, we can use the given information.
In this case, the initial concentration is C0 = 10 mg/L, and the concentration after 9 hours is C(t) = 3 mg/L. We need to find the value of r.
3 = 10 * e^(-r * 9)
0.3 = e^(-r * 9)
ln(0.3) = -r * 9
r = -ln(0.3) / 9 ≈ 0.192
Therefore, the value of r is approximately 0.192, which is option 3. 0.19.
|
ทฤษฎีของการย่อยยาในร่างกาย (Pharmacokinetics theory) ซึ่งเป็นส่วนหนึ่งของศาสตร์เภสัชวิทยา ทฤษฎีนี้ใช้ในการศึกษาและคาดการณ์การพึ่งพาของยาในร่างกาย โดยพิจารณาความเข้มข้นของยาในกระแสเลือดตามเวลา โดยใช้สูตร exponential function เพื่อบ่งชี้ถึงกระแสการลดลงของความเข้มข้นของยาในระยะเวลาที่ผ่านไป
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 13 |
Drug Concentrations
Exponential functions can be used to model the concentration of a drug in a patient’s body. Suppose the concentration of Drug X in a patient’s bloodstream is modeled by,
C (t) = Co e^(-rt),
จงหาสมการที่เป็นไปได้ หากยา x, มี r =0. 09 แล้วมีความเข้มข้นลดลง 80% จาก the model, C(t) = Co e^(-rt)
|
3. In 0.8 = -0.09t |
|
ในกรณีที่ยา X มีค่า r = 0.09 และความเข้มข้นลดลง 80% จากสมการ C(t) = Co e^(-rt) คือ
In 0.8 = -0.09t
เพื่อหาค่า t ในสมการนี้ เราสามารถใช้ฟังก์ชัน logarithm ฐาน e (natural logarithm) หรือ ln ได้ เนื่องจากเราต้องการแก้สมการสำหรับ t ที่เป็นกำลังของ e ในสมการนี้
ดังนั้น คำตอบที่ถูกต้องคือ No.3 In 0.8 = -0.09t
|
ทฤษฎีและหลักการใน Pharmacokinetics เกี่ยวข้องกับการศึกษาและการวิเคราะห์เกี่ยวกับกระบวนการของยาภายในร่างกาย เช่น การดูดซึม (Absorption) การกระจายตัว (Distribution) การเมตะบอลิซึม (Metabolism) และการขับถ่าย (Excretion) ซึ่งสามารถใช้ในการทำนายและรู้สึกสึกได้ถึงการเปลี่ยนแปลงของความเข้มข้นของยาในร่างกายตามเวลา
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 14 |
การกลายพันธุ์ของยีนใดที่อาจส่งผลต่อระดับ Warfarin
|
5. ไม่มีข้อถูก |
|
ยีน CYP2C9 เป็นยีนที่เข้ามามีบทบาทในการตรวจจับและแยกตัวสารอื่น ๆ เช่น Warfarin ในร่างกาย ซึ่งยีนนี้เกี่ยวข้องกับการตรวจจับและขนส่งยาภายในร่างกาย โดย CYP2C9 จะมีบทบาทในการแตกต่างความเร็วในการย่อยสลายยา Warfarin ในร่างกายของบุคคล หากมีการกลายพันธุ์ในยีน CYP2C9 อาจส่งผลต่อความไวต่อการย่อยสลายของ Warfarin ซึ่งอาจทำให้ระดับยาในเลือดเพิ่มขึ้นหรือลดลง และสามารถส่งผลต่อความเสี่ยงในการเกิดอาการนิ่วเลือดอันตรายได้
|
"ภาวะสมดุลย์พันธุกรรม" (Genetic Equilibrium) ภาวะสมดุลย์พันธุกรรมเกี่ยวข้องกับความสมดุลของอัลลีลคาร์ร์โนตัสในประชากร ภาวะนี้เกิดขึ้นเมื่อมีการควบคุมและความสมดุลของการสืบพันธุ์ และความถี่ของแต่ละแอลลีลคาร์ร์โนตัสยังคงเป็นค่าคงที่ในระยะยาว สมดุลย์พันธุกรรมเป็นฐานในการศึกษาความสัมพันธ์ระหว่างยีนและลักษณะทางสุขภาพ ในกรณีของ Warfarin, การกลายพันธุ์ในยีนที่เกี่ยวข้องกับการขับถ่ายหรือการย่อยยาอาจมีผลต่อระดับยาในร่างกายและอาจทำให้เกิดการตอบสนองทางสุขภาพที่แตกต่างกันในบุคคลต่างๆ โดยแอลลีลคาร์ร์โนตัสที่มีความแตกต่างอาจส่งผลต่อปริมาณยาที่ต้องใช้หรือปริมาณยาที่ต้องหลีกเลี่ยงเพื่อป้องกันความเสี่ยงจากการใช้ยา Warfarin โดยไม่เหมาะสม
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 15 |
เป็นเรื่องปกติที่จะให้ยา Warfarin ในขนาดเริ่มต้นที่แตกต่างกันกับผู้คนตามเชื้อชาติของพวกเขา หากให้น้อยเกินไปจะเกิดอะไรขึ้น
|
2. ทำให้เลือดออกมากเกินไป |
|
หากยา Warfarin ถูกให้ในขนาดเริ่มต้นที่น้อยเกินไป มีความเสี่ยงที่จะเกิดเลือดออกมากเกินไป (excessive bleeding) ซึ่งอาจเป็นอันตรายต่อผู้รับประทานยา ยา Warfarin มีส่วนบำรุงรักษาความเป็นเลือดลวก และถูกใช้ในการป้องกันการเกิดลิ่มเลือดในหลอดเลือด การให้ยาในขนาดที่น้อยเกินไปอาจทำให้เลือดมีความลวกน้อยลง ซึ่งอาจเป็นสาเหตุให้เลือดออกมากเกินไปเมื่อเกิดบาดเจ็บหรือฉีดสลายแขนงอื่นๆ ทำให้เกิดภาวะเลือดออก (hemorrhage) ได้ง่ายขึ้น
|
ทฤษฎีหลักคิดที่เกี่ยวข้องกับการให้ยา Warfarin ในขนาดที่แตกต่างกันกับผู้คนตามเชื้อชาติของพวกเขาเป็นส่วนหนึ่งของ Pharmacology และการทดลองทางคลินิก (Clinical Trials) ที่ได้รับการศึกษาและพิสูจน์ว่ายา Warfarin มีการส่งผลต่อระดับการแข็งตัวของเลือด (blood clotting) โดยผ่านการยับยั้งการสังเคราะห์วิตามิน K (Vitamin K) ในกระบวนการการสังเคราะห์แฟคเตอร์การแข็งตัวของเลือด (clotting factors) ซึ่งเป็นส่วนสำคัญในการเกิดการแข็งตัวของเลือด
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 16 |
ข้อใดไม่ใช่กลไกการออกฤทธิ์ของ Gleevac
|
5. ถูกมากกว่า 1 ข้อ |
|
เพราะข้อที่ 1, 2, 3 เป็นกลไกการออกฤทธิ์ของยา Gleevac ที่ถูกต้อง ซึ่งทั้งสามข้อนี้เป็นส่วนหนึ่งของการอธิบายกลไกการทำงานของยา Gleevac ในการปฏิบัติงานของมันในร่างกายเพื่อให้เข้าใจกลไกการออกฤทธิ์ของยาได้ดียิ่งขึ้น ดังนั้นข้อที่ว่า Gleevac ไม่มีกลไกการออกฤทธิ์ที่กล่าวถึงในข้อ 1, 2, 3 นั้นไม่ถูกต้อง
|
ยับยั้งโปรตีนฟิวชัน (Inhibition of Protein Fusion): Gleevac มีสารสำคัญชื่อ Imatinib ซึ่งสามารถยับยั้งโปรตีนฟิวชันในเซลล์มะเร็งได้ โดยเฉพาะอาการผิดปกติของโปรตีน BCR-ABL ซึ่งเกี่ยวข้องกับมะเร็งเม็ดเลือดขาวเฉพาะกลุ่ม (Chronic Myeloid Leukemia) และยังสามารถยับยั้งพันธะไฮโดรเจนเพื่อป้องกันการเจริญเติบโตของเซลล์มะเร็งอื่นๆได้ด้วย (Inhibition of other tyrosine kinases).
ผ่านฟอสโฟรีเลชัน (Phosphorylation): Gleevac มีสารสำคัญชื่อ Imatinib ที่สามารถผ่านฟอสโฟรีเลชันในเซลล์มะเร็ง ซึ่งสามารถยับยั้งเอนไซม์ที่เกี่ยวข้องกับการสร้างฟอสโฟรีเลตในเซลล์มะเร็งได้ ทำให้เกิดผลในการยับยั้งการเจริญเติบโตของเซลล์มะเร็ง.
ช่วยให้เซลล์มะเร็งแพร่กระจาย (Inhibition of Cell Proliferation): Gleevac ช่วยยับยั้งการแบ่งเซลล์และการเจริญเติบโตของเซลล์มะเร็ง โดยเฉพาะกลุ่มของเซลล์มะเร็งที่มีการเจริญเติบโตอย่างรวดเร็ว.
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 17 |
ข้อใดไม่เกี่ยวข้องกับการขาดกลูโคส -6- ฟอสเฟต G6PD?
|
4. ความเครียด |
|
การขาดกลูโคส-6-ฟอสเฟต G6PD เป็นโรคยีนสมองชนิดหนึ่งที่ส่งผลให้เซลล์เม็ดเลือดแดงที่มีเอนไซม์ G6PD ขาดสามารถทำงานได้อย่างไม่เพียงพอในการสังเคราะห์สารเคมีที่จำเป็นต่อการปกป้องเม็ดเลือดแดงจากการทำลายของสารออกซิเดชัน
|
การขาดกลูโคส-6-ฟอสเฟต G6PD อาจเป็นสาเหตุให้มีการทำลายเม็ดเลือดแดงเพิ่มขึ้น เรียกว่าฮีโมลิติก เม็ดเลือดแดงที่ขาดกลูโคส-6-ฟอสเฟต G6PD ไม่สามารถสร้างสาร NADPH ที่จำเป็นต่อการทำซ้ำกระบวนการทางต่างๆ ในเม็ดเลือดแดง ซึ่ง NADPH เป็นสารที่ช่วยในกระบวนการปกป้องเซลล์จากการทำลายและช่วยซ่อมแซมสารต่างๆ ภายในเซลล์
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 18 |
ข้อใดไม่ได้อธิบายสมมติฐาน Life on the Edge ที่เกี่ยวข้องกับโรคอะไมลอยด์
|
3. ธรรมชาติของโพลีเปปไทด์ |
|
สมมติฐาน "Life on the Edge" ไม่ได้ระบุเกี่ยวกับธรรมชาติของโพลีเปปไทด์ หรือโครงสร้างของโปรตีนดังกล่าว
|
สมมติฐาน "Life on the Edge" เน้นไปที่ความซับซ้อนและลักษณะทั่วไปของระบบที่มีการเชื่อมโยงระหว่างขนาดและความซับซ้อนของระบบต่างๆในการเติบโตและพัฒนา
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 19 |
ข้อใดเกี่ยวข้องกับ Environmental toxicology
|
5. ถูกมากกว่า 1 ข้อ |
|
ทั้งหมดข้อ 1, 2, 3, และ 4 เกี่ยวข้องกับ Environmental toxicology โดยที่:
Pesticide Dichlorodiphenyltrichloroethane (DDT): DDT เป็นสารเคมีฆ่าแมลงที่มีผลกระทบต่อสิ่งแวดล้อมและมนุษย์ เป็นต้นไป
Industrial Chemicals: สารเคมีที่ใช้ในอุตสาหกรรมสามารถเป็นพิษต่อสิ่งแวดล้อมและมนุษย์ได้
PCBs (Polychlorinated Biphenyls): PCBs เป็นสารเคมีหนึ่งที่ใช้ในอุตสาหกรรมและสามารถก่อให้เกิดปัญหาสุขภาพและมีผลกระทบต่อสิ่งแวดล้อม
PFAS (Per- and Polyfluoroalkyl Substances): PFAS เป็นกลุ่มของสารเคมีที่ใช้ในหลายอุตสาหกรรมและสามารถมีผลกระทบต่อสิ่งแวดล้อมและสุขภาพมนุษย์ได้
|
***Environmental toxicology เกี่ยวข้องกับการศึกษาและการวิจัยเกี่ยวกับผลกระทบของสารเคมีต่อสิ่งแวดล้อมและมนุษย์ ซึ่งสามารถอ้างอิงถึงหลายทฤษฎีและแนวคิดต่าง ๆ ได้ เช่น:
-------
-หลักการของความพิการ (Principle of Disability): ทฤษฎีนี้เน้นการศึกษาผลกระทบที่เกิดจากสารเคมีต่อสิ่งแวดล้อมและสิ่งมีชีวิตในระดับต่าง ๆ โดยพิจารณาผลกระทบที่เกิดกับฟังก์ชันของระบบชีววิทยาและสิ่งมีชีวิตต่าง ๆ
-หลักการของความเป็นพิษ (Principle of Toxicity): ทฤษฎีนี้เน้นการศึกษาและวิเคราะห์สารเคมีว่ามีความพิษและผลกระทบอย่างไรต่อสิ่งมีชีวิต โดยพิจารณาจากปริมาณที่ต่อเนื่องและความเข้มข้นของสาร
-หลักการของความเสี่ยง (Principle of Risk): ทฤษฎีนี้เน้นการประเมินความเสี่ยงที่เกี่ยวข้องกับการใช้สารเคมี และการจัดการความเสี่ยงเพื่อลดผลกระทบต่อสิ่งแวดล้อมและมนุษย์
-หลักการของความหลากหลายทางชีวภาพ (Principle of Biodiversity): ทฤษฎีนี้เน้นการศึกษาและการเข้าใจถึงความหลากหลายทางชีวภาพของสิ่งมีชีวิตที่สามารถถูกผลกระทบจากสารเคมีได้
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 20 |
จาก Engineered brain-targeted drug delivery systems ที่ใช้คืออะไร
|
1. DOX in liposomes |
|
Engineered brain-targeted drug delivery systems ที่ใช้เพื่อการส่งยาเข้าสู่สมองสามารถมีหลายวิธี โดยตัวเลือกที่ได้รับความสนใจมากที่สุดคือ Liposomes
|
Engineered brain-targeted drug delivery systems ที่ใช้เพื่อการส่งยาเข้าสู่สมองสามารถมีหลายวิธี โดยตัวเลือกที่ได้รับความสนใจมากที่สุดคือ Liposomes ซึ่งเป็นกลไกการส่งยาที่ใช้ในการเจาะเข้าสู่สมองโดยการใช้แนวคิดของยาในแว่นพลาสมาเนตกลุ่มซ้อน ๆ ที่เรียกว่า Liposomes เพื่อให้ยาสามารถผ่านประตูเซลล์ของสมองและถึงจุดเป้าหมายในสมองได้โดยตรง
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|