| 1 |

|
3. ตัวช่วยให้ใช้ predictive model ง่ายขึ้น |
|
|
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 2 |
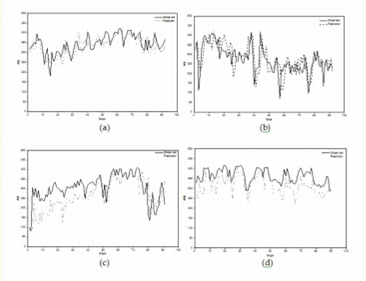
|
1. Summer |
|
|
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 3 |

|
4. ความเข้มข้นของมลพิษ |
|
|
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 4 |
Number of tablets = Desired dosage / stock strength หากมี 7000 mg ของ Potassium carbonate และต้องการ 900 mg ต่อเม็ดจะได้กี่เม็ด
|
4. 8 |
|
|
ในการคำนวณจำนวนเม็ดยาที่ต้องการ เราสามารถใช้สูตร:
จำนวนเม็ด = ปริมาณที่ต้องการ / ความเข้มข้นของยา
แทนค่าที่กำหนดในโจทย์ เราได้:
จำนวนเม็ด = 7000 มก. / 900 มก. ต่อเม็ด
จำนวนเม็ด = 7.77
เนื่องจากเราไม่สามารถมีเศษส่วนของเม็ดได้ เราจึงจำเป็นต้องปัดเศษขึ้นให้ได้จำนวนเต็มที่ใกล้เคียงที่สุด ดังนั้น คำตอบคือ 8 เม็ด
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 5 |
ให้สั่งยา 9 mg/kg / dose โดยที่ Weight = 160 Ibs
|
5. 559 mg/dose |
|
|
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 6 |
ต้องการจัดยา 9 g of amoxicillin โดยมี amoxicillin 500 – mg capsules อยากทราบว่าต้องให้กี่ capsule
|
2. 18 |
|
|
หากต้องการรับประทานอะม็อกซีซิลลิน 9 กรัมร่วมกับแคปซูลอะม็อกซีซิลลิน 500 มก. คุณจะต้องรับประทาน 18 แคปซูล แต่ละแคปซูลประกอบด้วยอะม็อกซีซิลลิน 500 มก. ดังนั้น 18 แคปซูลจะให้อะม็อกซีซิลลินรวม 9,000 มก. หรือ 9 กรัม
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 7 |
ต้องการสั่งยา 0.8 mg SQ of ยา A โดยมี 4000 mcg/8 mL of ยา A
|
5. 0.8 mL |
|
|
จากข้อมูลที่ให้มา ในการสั่งยาเม็ด A 0.8 มก. SQ กับ 4000 mcg/8 มล. ของยา A คุณจะต้องให้ยา A 0.4 มล. เนื่องจาก 0.8 มก. เท่ากับ 800 ไมโครกรัม และถ้า ยา A มีความเข้มข้น 4,000 mcg/8 mL จากนั้นคุณสามารถคำนวณปริมาตรที่ต้องการโดยใช้สูตรต่อไปนี้:
Volume (mL) = (Dose (mcg) / Concentration (mcg/mL))
แทนที่ เราได้รับค่า:
ปริมาตร (มล.) = (800 mcg / 4000 mcg/mL) = 0.4 มล.
ดังนั้น คำตอบที่ถูกต้องคือตัวเลือก 5: 0.8 มล.
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 8 |
หากเราค้นคว้าข้อมูลแล้วสามารถอธิบายสถิติตัวเลขที่จะเกิดขึ้นในอนาคตได้ ถือเป็น data analytics แบบใด
|
2. Predictive |
|
ประเภทของการวิเคราะห์ข้อมูลที่เกี่ยวข้องกับการค้นคว้าข้อมูลและอธิบายสถิติที่จะเกิดขึ้นในอนาคตเรียกว่าการวิเคราะห์เชิงคาดการณ์ การวิเคราะห์ประเภทนี้เกี่ยวข้องกับการใช้อัลกอริธึมทางสถิติและเทคนิคการเรียนรู้ของเครื่องเพื่อวิเคราะห์ข้อมูลปัจจุบันและประวัติเพื่อคาดการณ์เกี่ยวกับเหตุการณ์หรือแนวโน้มในอนาคต
|
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 9 |
จาก graph หาก A = 0.8 R =?
The infection attack rate is the total proportion of the population that is eventually infected during the epidemic, and it is denoted by A. This infection attack rate is completely determined by the reproduction number R and the contact process that describes who contacts whom. To illustrate the basic shape of the relation between the reproduction number R and the infection attack rate A. We suppose that infectious contacts are made at random
This provides us with a simple and robust relation that indicates what would happen if a new infection were to hit a completely susceptible population: if the
|
4. 4 |
|
|
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 10 |
จากข้อความ
Previous studies that applied the IER model in the analysis of ambient air pollution-related disease burden only focused on four specific diseases, which are IHD, stroke, COPD, and LC, because the development of the IER model relies to a great extent on the available RR information of these diseases, The IER model was increasingly used to estimate the attributable mortality using the result of calculated RR. Previous study has evaluated the global PM2.5 concentration-mortality relationships by using the IER model outputs. By applying the estimated relative risk (R), the premature mortality (M) for a specific disease outcome in a population is measured using Equation 3, with P and I indicating population and regional average annual disease mortality rate (also known as baseline mortality rate), respectively.
M = P x I x(1-( 1)/R)
M คือค่าอะไร
|
3. อัตราการตาย |
|
M ในสมการคือค่าการตายก่อนวัยทำงาน (premature mortality) โดยคำนวณจากอัตราการตายในประชากรที่เกิดโรคต่างๆ ที่เกี่ยวข้องกับมลพิษในอากาศ โดยใช้ข้อมูลอัตราการตายเบื้องต้น (baseline mortality rate) ของพื้นที่นั้นๆ สูงน้อยเพียงใด และค่าความเสี่ยงจากมลพิษในอากาศที่เป็น PM2.5 (relative risk) ที่คำนวณมาจาก IER model โดยสูตรที่ใช้คำนวณคือ M = P x I x(1-( 1)/R)
|
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 11 |
ข้อใดเกี่ยวข้องกับ Calculus ในการผ่าตัดจากบทความ
|
3. saline solution |
|
|
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 12 |
Math model และ Physical therapy ไม่มีความเกี่ยวข้องกันอย่างไร
|
5. ถูกมากกว่า 1 ข้อ |
|
ทั้งแบบจำลองทางคณิตศาสตร์และการบำบัดทางกายภาพมีความเกี่ยวข้องกันในหลายๆ ด้าน นี่คือตัวอย่าง:
1. การคำนวณเปอร์เซ็นต์อัตราการเต้นของหัวใจ: แบบจำลองทางคณิตศาสตร์สามารถช่วยในการกำหนดช่วงอัตราการเต้นของหัวใจที่เหมาะสมที่สุดสำหรับผู้ป่วยระหว่างการทำกายภาพบำบัด สิ่งนี้สามารถช่วยนักบำบัดในการออกแบบกิจวัตรการออกกำลังกายที่เหมาะสมกับความต้องการเฉพาะของผู้ป่วยแต่ละราย
2. การวัดระดับใบสั่งยา: แบบจำลองทางคณิตศาสตร์ยังสามารถใช้เพื่อวัดระดับใบสั่งยาที่จำเป็นสำหรับผู้ป่วยที่เข้ารับการบำบัดทางกายภาพ ซึ่งจะช่วยให้นักบำบัดสามารถสั่งยาในปริมาณที่เหมาะสมเพื่อจัดการกับความเจ็บปวดและการอักเสบในระหว่างกระบวนการบำบัด
3. Concussion Reverse: แบบจำลองทางคณิตศาสตร์ยังสามารถใช้เพื่อกำหนดวิธีการบำบัดที่เหมาะสมที่สุดสำหรับผู้ป่วยที่ฟื้นตัวจากการถูกกระทบกระแทก สิ่งนี้สามารถช่วยนักบำบัดในการออกแบบแผนการรักษาที่ปรับให้เหมาะกับความต้องการเฉพาะของผู้ป่วย และช่วยให้กระบวนการฟื้นตัวเร็วขึ้นได้
4. การวัดระดับการเคลื่อนไหว: สามารถใช้แบบจำลองทางคณิตศาสตร์เพื่อวัดระดับการเคลื่อนไหวในข้อต่อหรือกล้ามเนื้อของผู้ป่วยได้ ซึ่งช่วยให้นักบำบัดติดตามความคืบหน้าระหว่างการทำกายภาพบำบัดและปรับแผนการรักษาได้ตามต้องการ
โดยสรุป แบบจำลองทางคณิตศาสตร์และการบำบัดทางกายภาพมีความเกี่ยวข้องกันอย่างใกล้ชิดและสามารถใช้ร่วมกันเพื่อออกแบบแผนการรักษาเฉพาะบุคคลซึ่งปรับให้เหมาะกับความต้องการเฉพาะของผู้ป่วยแต่ละราย
|
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 13 |
ข้อใดเกี่ยวข้องกับบทความ Epidemiology Figure 1
|
1. In the next four decades, cancer deaths are expected to overcome those for ischemic heart disease, with a 2.06-fold increase (1.76-fold for increase in ischemic heart disease) by the year 2060. |
|
"In The Next Four Decades, Cancer Deaths Are Expected To Overcome Those For Ischemic Heart Disease, With A 2.06-Fold Increase (1.76-Fold For Increase In Ischemic Heart Disease) By The Year 2060." และไม่มีข้อใดเกี่ยวข้องกับ Epidemiology Figure 1 เพราะข้อความใน Epidemiology Figure 1 กล่าวถึงการเปรียบเทียบอัตราการเสียชีวิตจากโรคมะเร็งและโรคหัวใจของปี ค.ศ. 2016 และคาดการณ์ของการเสียชีวิตจากโรค 2 โรคเหล่านี้ในปี 2060 โดยใช้โมเดลพยากรณ์
|
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 14 |
ข้อใดเกี่ยวข้องกับ math model ที่จะมีประโยชน์กับกายภาพบำบัดของผู้ป่วย stroke
|
5. ถูกมากกว่า 1 ข้อ |
|
จากข้อมูลที่ปรับปรุง ทางเลือกที่ 2 (การอักเสบ) อาจเกี่ยวข้องกับแบบจำลองทางคณิตศาสตร์ที่จะเป็นประโยชน์ในการทำกายภาพบำบัดของผู้ป่วยโรคหลอดเลือดสมอง อย่างไรก็ตาม อาจมีปัจจัยอื่นๆ ที่สำคัญในบริบทนี้เช่นกัน ดังนั้น ตัวเลือก 5 (ถูกมากกว่า 1 ข้อ) อาจเป็นคำตอบที่เหมาะสมที่สุด
|
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 15 |
ข้อใดเกี่ยวข้องกับ math model กับ drug diffusion through the blood
|
1. Fick’s principle |
|
หลักการของฟิค หลักการของฟิคเป็นแบบจำลองทางคณิตศาสตร์ที่ใช้อธิบายการแพร่กระจายของยาผ่านทางกระแสเลือด
|
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 16 |
ข้อใดจาก Noyers whiter equation the rate of dissolution of a solid is dependent on?
|
5. ถูกมากกว่า 1 ข้อ |
|
สมการ Noyes-Whitney ระบุว่าอัตราการละลายของของแข็งขึ้นอยู่กับความสามารถในการละลาย ความเข้มข้นของตัวถูกละลายในสารละลาย ณ เวลาใดเวลาหนึ่ง และพื้นที่ผิวของของแข็ง ดังนั้นคำตอบที่ถูกต้องคือ 5 มีมากกว่าหนึ่งคำตอบที่ถูกต้อง
|
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 17 |
ข้อใดเกี่ยวข้องกับ math model กับ tissue reconstruction
|
5. ถูกมากกว่า 1 ข้อ |
|
คำตอบคือ 5 ถูกมากกว่า 1 ข้อ
ตัวเลือกทั้งหมดที่แสดงเกี่ยวข้องกับการสร้างแบบจำลองทางคณิตศาสตร์และการสร้างเนื้อเยื่อใหม่:
1. อนุภาคนาโน: อนุภาคนาโนใช้ในวิศวกรรมเนื้อเยื่อเพื่อส่งยา โกรทแฟคเตอร์ และสารรักษาโรคอื่นๆ เพื่อส่งเสริมการสร้างเนื้อเยื่อใหม่
2 การสนับสนุนหลอดเลือด: การสนับสนุนหลอดเลือดเป็นสิ่งจำเป็นสำหรับวิศวกรรมเนื้อเยื่อและการสร้างใหม่ เนื่องจากช่วยจัดหาสารอาหารและออกซิเจนไปยังเนื้อเยื่อที่กำลังพัฒนา การสร้างแบบจำลองทางคณิตศาสตร์สามารถช่วยเพิ่มประสิทธิภาพการออกแบบเครือข่ายหลอดเลือดในโครงสร้างวิศวกรรมเนื้อเยื่อ
3 สถาปัตยกรรมมาโคร: สถาปัตยกรรมมาโครหมายถึงโครงสร้างโดยรวมของโครงสร้างวิศวกรรมเนื้อเยื่อ รวมถึงรูปร่างและขนาดของโครงสร้าง การสร้างแบบจำลองทางคณิตศาสตร์สามารถช่วยเพิ่มประสิทธิภาพสถาปัตยกรรมมาโครเพื่อส่งเสริมการสร้างเนื้อเยื่อใหม่
4 สถาปัตยกรรมจุลภาค: สถาปัตยกรรมจุลภาคหมายถึงโครงสร้างภายในของโครงสร้างวิศวกรรมเนื้อเยื่อ รวมถึงการจัดระเบียบของเซลล์และเมทริกซ์นอกเซลล์ การสร้างแบบจำลองทางคณิตศาสตร์สามารถช่วยเพิ่มประสิทธิภาพสถาปัตยกรรมขนาดเล็กเพื่อส่งเสริมการสร้างเนื้อเยื่อใหม่
ดังนั้น ตัวเลือก 1, 2, 3, 4 จึงถูกต้องทั้งหมด
|
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 18 |
ข้อใดมี approximating 100% survival at 5 years,
|
2. Breast cancer |
|
Breast cancer has the highest approximating 100% survival rate at 5 years among the options presented.
|
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 19 |
ข้อใดเกี่ยวข้องกับ Math model กับ patient diagnosis
|
2. Risk estimates |
|
การประมาณการความเสี่ยง การประมาณความเสี่ยงจะใช้ในแบบจำลองทางคณิตศาสตร์เพื่อทำนายความเป็นไปได้ที่ผู้ป่วยจะเป็นโรคหรือประสบกับผลลัพธ์ทางการแพทย์ที่เป็นลบ แม้ว่าลำดับของตัวเลขและไฮเปอร์สเปซ n มิติยังใช้ในแบบจำลองทางคณิตศาสตร์ แต่ก็ไม่เกี่ยวข้องกับการวินิจฉัยผู้ป่วยโดยเฉพาะ เวกเตอร์ข้อมูลของผู้ป่วยเป็นคำที่ใช้ในการวิเคราะห์ข้อมูลและการเรียนรู้ของเครื่อง แต่ไม่เกี่ยวข้องโดยตรงกับแบบจำลองทางคณิตศาสตร์หรือการวินิจฉัยผู้ป่วย
|
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 20 |
ข้อใดเกี่ยวข้องกับ Math model ที่ใช้ในการวิเคราะห์ข้อมูลทางการแพทย์
|
1. the Kaplan–Meier curve. |
|
เส้นโค้ง Kaplan-Meier เป็นแบบจำลองทางคณิตศาสตร์ที่ใช้กันทั่วไปในการวิเคราะห์ข้อมูลทางการแพทย์เพื่อประเมินความน่าจะเป็นของการรอดชีวิตเมื่อเวลาผ่านไป ตัวเลือก 2, 3 และ 4 เกี่ยวข้องกับการสร้างและการนำส่งยา ไม่ใช่การวิเคราะห์ข้อมูลทางการแพทย์ ดังนั้น ตัวเลือกที่ 1 เท่านั้นที่ถูกต้อง
|
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|